Dispersion vs Diffusion – Taylor Dispersion

Dispersion and diffusion are commonly misunderstood. Both refer to a “spreading” phenomenon but have different mechanisms. Diffusion results from the random motion of molecules and is characterised by a diffusion coefficient, $D_a$. Dispersion on the other hand results from the variable flow-path of a fluid.

To illustrate, let’s look at Taylor dispersion for steady laminar flow in a long pipe with a Poiseuille flow radial velocity distribution:

$$u = U_0(1 - \frac{r^2}{R^2})$$

Giving rise to the following shape:

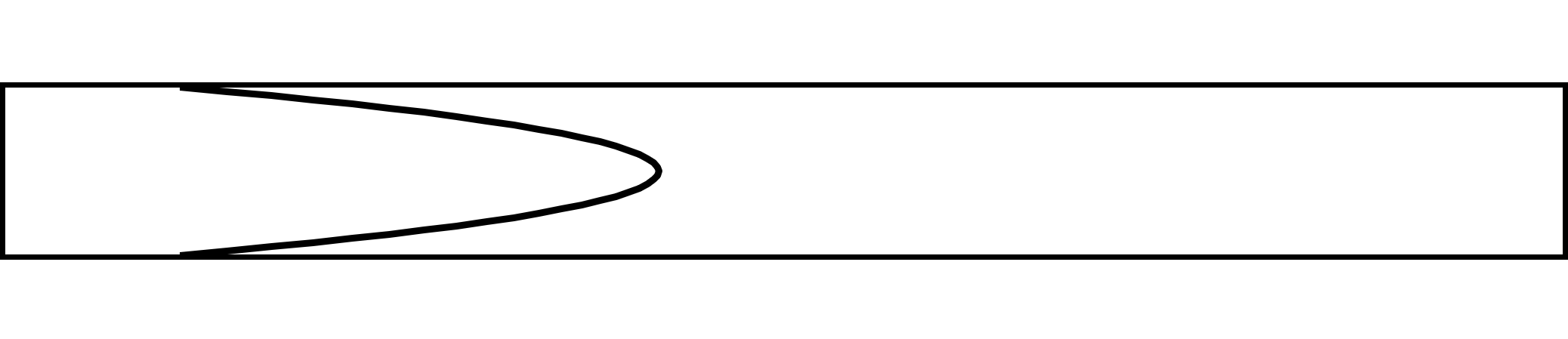
Suppose we fill the pipe with species A between two planes at a known concentration. Taylor assumed that the axial molecular diffusion is negligible compared to the radial molecular diffusion. After time $t$ there will be two concentration fronts:

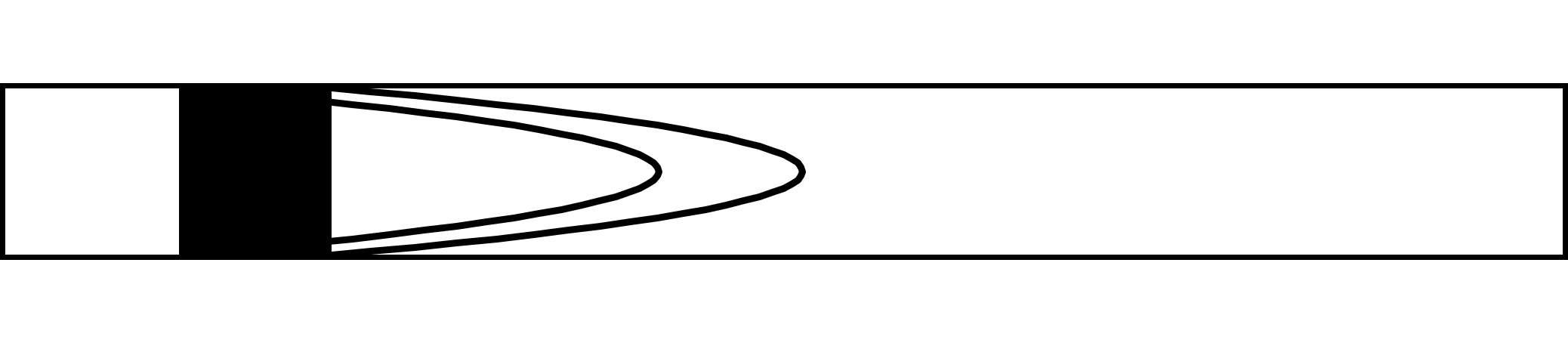
Rapid spreading of the tracer in the radial direction results in a profile like so:

Therefore, the dispersed concentration profile is caused by the velocity profile, and not due to axial molecular diffusion.

The axial dispersion coefficient falls out of this analysis as:

$$D_{ax} = \frac{R^2U_0^2}{192D_a}$$

Importantly, $D_{ax}$ is not a property of the fluid and depends on the pipe radius and mean velocity. In fact, $D_{ax}$ is inversely proportional to the diffusion coefficient!

Accounting for axial molecular diffusion Aris modified the equation for Taylors axial dispersion coefficient to be:

$$D_{ax} = D_a + \frac{R^2U_0^2}{192D_a}$$

Taylor dispersion is ubiquitous in chemical engineering and important for gas separation using structured adsorbents – a future topic.